Floating-point numbers

Floating-point number representation

• For example, 312110000000000000000000 can be written as $3.1211\times {10}^{23}$ using scientific notation.

• If we adopt this system in binary, we get:

$$M\times 2^E$$

• M is the mantissa and E is the exponent.

• This is known as binary floating-point representation.

• In our examples, we will assume a computer is using 8bits to represent the mantissa and 8bits to store the exponent (a binary point is assumed to exist between the first and second bits of the mantissa).

• Again, using denary as our example, a number such as $0.31211\times {10}^{24}$ means:

• We thus get the binary floating-point equivalent (using 8 bits for the mantissa and 8 bits for the exponent with the assumed binary point between –1 and 1/2 in the mantissa):

Floating-point numbers

In binary, we use $Mimes{2}^E$ to represent floating-point numbers, M is the and E is the .

[0/2]

Convert this binary floating-point number into denary

• For exmaple: 0101 1010 0000 0100

Method 1

• M = 1/2 + 1/8 + 1/16 + 64/1 = 45/64

• E = 4

• $M\times 2^E$

• = 45/64 x 24

• = 0.703125 x 16

• = 11.25

Method 2

• M = 0.1011010
• E = 4

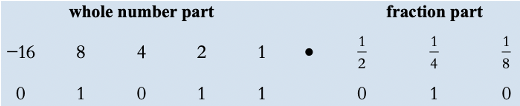
• Shift point to right with 4 digit: 01011.010

• = 8 + 2 + 1 + 1/4 + 1/8

• = 11.25

Floating-point numbers

Convert this binary floating-point number into denary:0010 1000 0000 0011

[0/1]

Converting denary numbers into binary floating-point numbers

• Convert +4.5 into a binary floating-point number.

Method 1

• 4.5 = 9/2 = 9/16 x 2³
• M = 9/16 = 1/2 + 1/16
• E = 3

• M = 01001000
• E = 00000011

Ans: 01001000.00000011

Method 2

• 4 = 0100 and .5 = .1 which gives: 0100.1

• 0100.1 = 0.1001 x 11(moving three(11) places left)

Ans: 01001000.00000011

Floating-point numbers

Converting denary numbers into binary floating-point numbers:0.171875

[0/1]

Normalisation

0.1000000 00000010	=1/2*22	=2
0.0100000 00000011	=1/4*23	=2
0.0010000 00000100	=1/8*24	=2
0.0001000 00000101	=1/16*25	=2

• With this method, for a positive number, the mantissa must start with 0.1 (as in our first representation of 2 above).

• The bits in the mantissa are shifted to the left until we arrive at 0.1; for each shift left, the exponent is reduced by 1.

• Look at the examples above to see how this works (starting with 0.0001000 we shift the bits 3 places to the left to get to 0.100000 and we reduce the exponent by 3 to now give 00000010, so we end up with the first representation!).

• For a negative number the mantissa must start with 1.0.

• The bits in the mantissa are shifted until we arrive at 1.0; again, the exponent must be changed to reflect the number of shifts.

Floating-point numbers

With this method, for a positive number, the mantissa must start with , for a negative number the mantissa must start with

[0/2]

Potential rounding errors and approximations

• .88 × 2 = 1.76 so we will use the 1 value to give 0.1

• .76 × 2 = 1.52 so we will use the 1 value to give 0.11

• .52 × 2 = 1.04 so we will use the 1 value to give 0.111

• .04 × 2 = 0.08 so we will use the 0 value to give 0.1110

• .08 × 2 = 0.16 so we will use the 0 value to give 0.11100

• .16 × 2 = 0.32 so we will use the 0 value to give 0.111000

• .32 × 2 = 0.64 so we will use the 0 value to give 0.1110000

• .64 × 2 = 1.28 so we will use the 1 value to give 0.11100001

• 5.88 = 0101.11100001 = 0.1011100 00000011 = 23/32 x 23 = 23/4 = 5.75

• So, 5.88 is stored as 5.75 in our floating-point system.

Precision vs Range

• The accuracy of a number can be increased by increasing the number of bits used in the mantissa.
• The range of numbers can be increased by increasing the number of bits used in the exponent.
• Accuracy and range will always be a trade-off between mantissa and exponent size.

TIP

• The mantissa is 12 bits and the exponent is 4 bits. This gives a largest positive value of (2047/2048)x27; which gives high accuracy but small range.

TIP

• The mantissa is 4 bits and the exponent is 12 bits. This gives a largest possible value of (7/8)×22047, which gives poor accuracy but extremely high range.

Floating-point numbers

The accuracy of a number can be increased by increasing the number of bits used in the , the range of numbers can be increased by increasing the number of bits used in the

[0/2]

Overflow and underflow

• There are additional problems:
  • If a calculation produces a number which exceeds the maximum possible value that can be stored in the mantissa and exponent, an overflow error will be produced. This could occur when trying to divide by a very small number or even 0.
  • When dividing by a very large number this can lead to a result which is less than the smallest number that can be stored. This would lead to an underflow error.
  • One of the issues of using normalised binary floating-point numbers is the inability to store the number zero. This is because the mantissa must be 0.1 or 1.0 which does not allow for a zero value.

Floating-point numbers

If a calculation produces a number which exceeds the maximum possible value that can be stored in the mantissa and exponent, an error will be produced. When dividing by a very large number this can lead to a result which is less than the smallest number that can be stored. This would lead to an error

[0/2]